
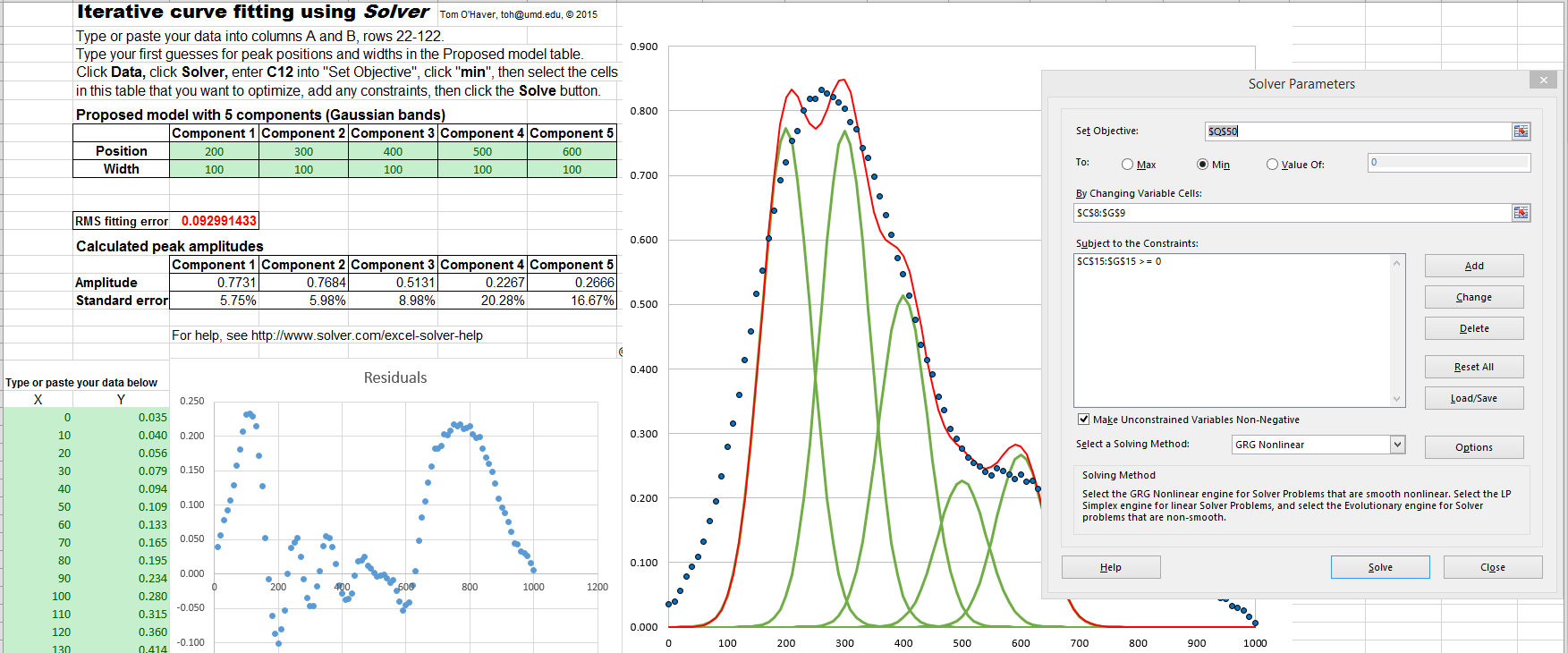
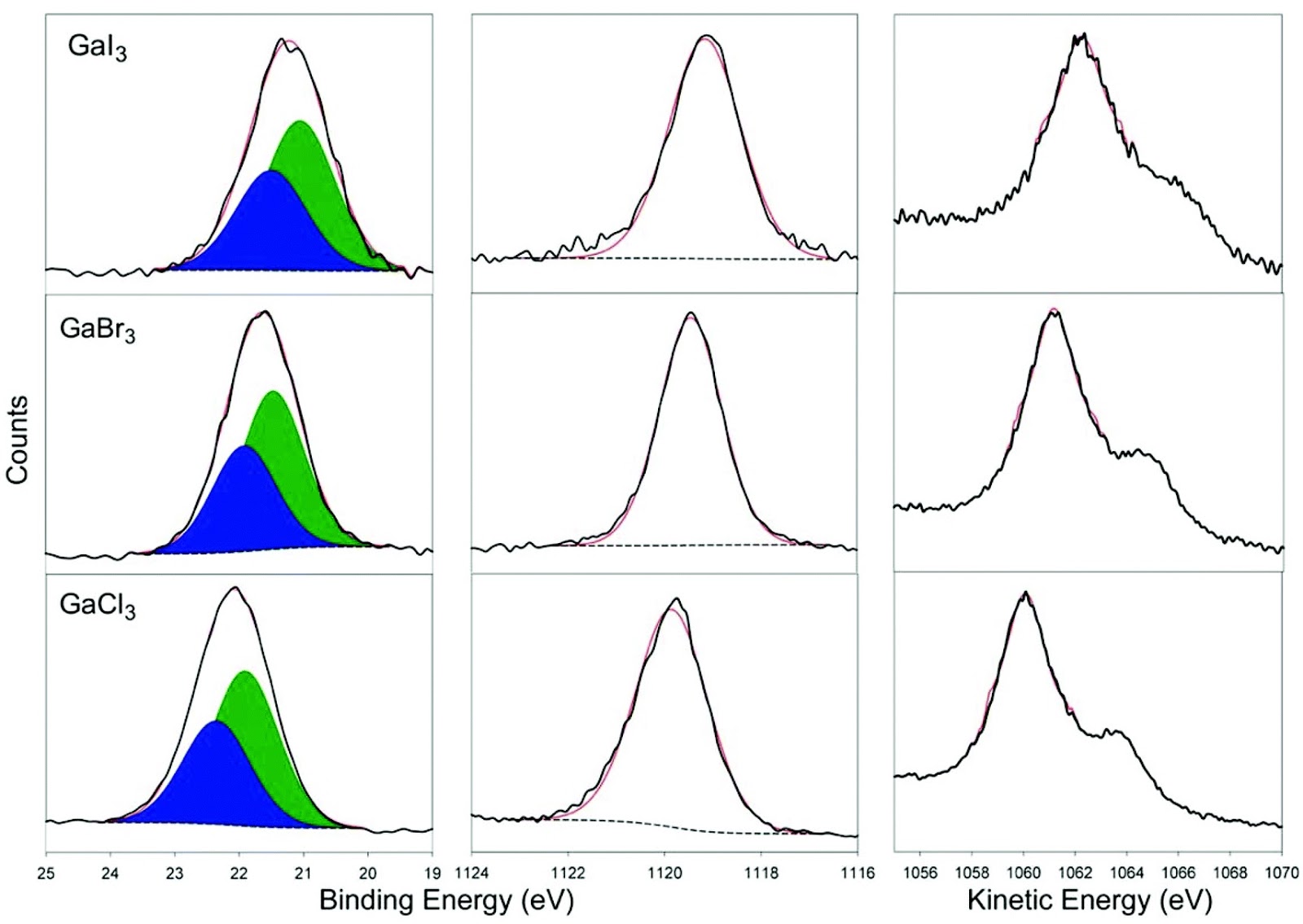
To recap: this iteration does not need to know how many peaks there are nor where they are located. In this data, (since there really only are two peaks) applying the process again will just give more (and smaller) peaks which can be weeded out by some kind of threshold, perhaps chosen from a knowledge of the noise floor. This shows the detected maxima (the orange dots) and the fitted normal exponentials along with the data. Where the data is a list of points like ]] I am expecting something like this: PeakFit:=. (I am aware of fitting functions like FindFit, NonlinearModelFit etc., so my question is more about how to build the model and estimate the initial parameters for input of the fitting functions.) Is there a Mathematica function that can simply do this? Or if anyone can give an idea of how to do the multi-peak fitting using Mathematica. The number of peaks is unknown and should be detected automatically, and the fitting model must also be built accordingly. The peak model is given and fixed (all peaks are fitted by the same model), but its particular form (which will be input) can be Gaussian or Lorentzian or some other customized functions. Following is an example of fitting the data using three peaks (such that the data ~ peak1 + peak2 + peak3). I am wondering how to implement the multi-peak detecting and fitting in Mathematica.


 0 kommentar(er)
0 kommentar(er)
